Elastic mesh
Problem 4
We have a rectangular mesh in the plane consisting of nodes that are connected to their neighbours with ideal springs. There are $100\times 100$ nodes in the web that are labeled with pairs $(i,j)$ of integres from $1$ to $100$. Two nodes $(i, j)$ and $(k, l)$ are connected if one of the indices conincides and the other differ by one (either $i = k$ and $|j-l|=1$ or $|i-k|=1$ and $j=l$).
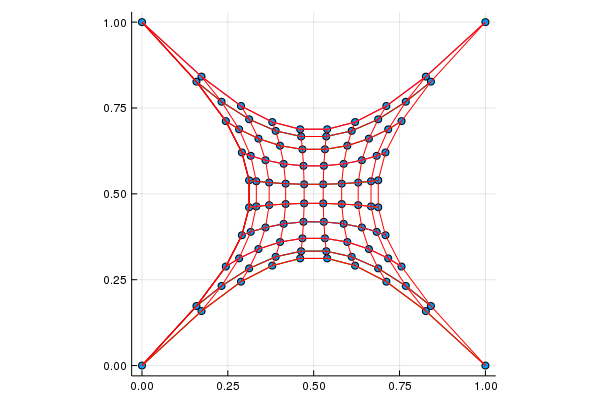
Example of a 10 by 10 mesh
We assume that the force by the spring, that connects two nodes with coordinates $(x_1, y_1)$ and $(x_2, y_2)$ is proportional to the distance between the nodes. The vector representing the force that the spring exerts on the first node is
where $k$ is the same for all the strings.
We fix the corners of the mesh in points $(0,0)$, $(1,0)$, $(1,1)$ and $(0,1)$ and let other nodes assume the static position where all the forces cancel. What is the distance from the corner to the first neighbour?