Elastična mreža
Naloga 4
V ravnini imamo pravokotno mrežo v kateri so vozlišča povezana z idealnimi vzmetmi. V mreži je $100\times 100$ vozlišč, ki so označene s pari naravnih števil $(i,j)$ med $1$ in $100$. Dve vozlišči $(i, j)$ in $(k, l)$ sta povezani, če se ena indeksa ujemata in se druga indeksa razlikujeta za ena (bodisi $i = k$ in $|j-l|=1$ ali $|i-k|=1$ in $j=l$).
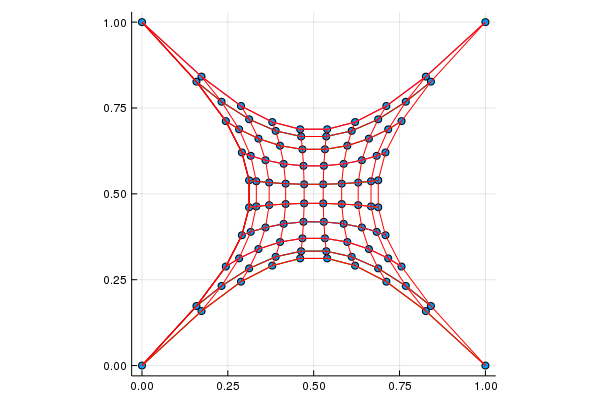
Primer mreže 10 krat 10
Predpostavimo, da je sila vzmeti, ki povezuje dve vozlišči s kooridinatami $(x_1, y_1)$ in $(x_2, y_2)$ sorazmerna razdalji med vozlišči. Vektor, ki predstavlja silo vzmeti na prvo vozlišče lahko zapišemo kot
kjer je $k$ koeficient vzmeti, ki je enak za vse vzmeti.
Vogale mreže postavimo v točke $(0,0)$, $(1,0)$, $(1,1)$ in $(0,1)$ in pustimo, da se ostala vozlišča postavijo v negiben položaj, v katerem se vse sile izničijo. Koliko je razdalja med vogalom in najbližjim vozliščem?